形式语言与自动机
前言
- 形式语言理论:乔姆斯基发现文法,用文法产生语言的每个句子。
- 自动机理论:克林建立了有穷状态自动机,为识别语言的系统
- 文法与自动机是等价的
- 文法与自动机的运算对象:集合

文法
文法构造
例1
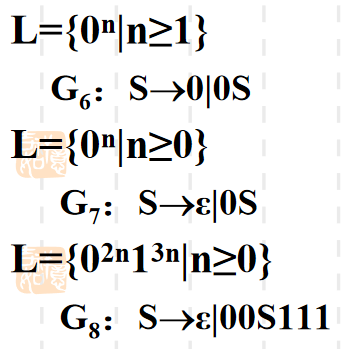
例2
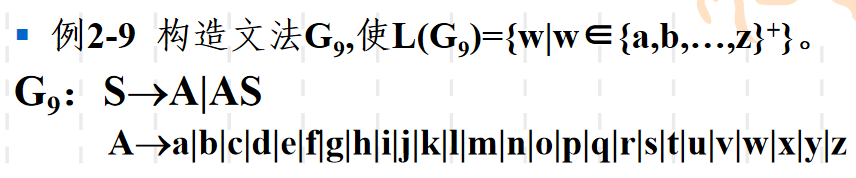
例3
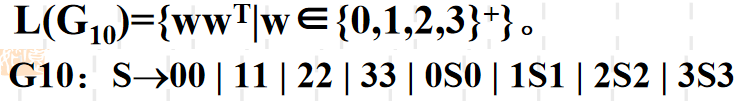
例4


例5

例6
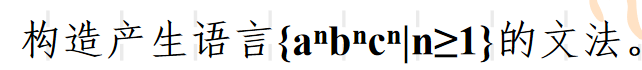
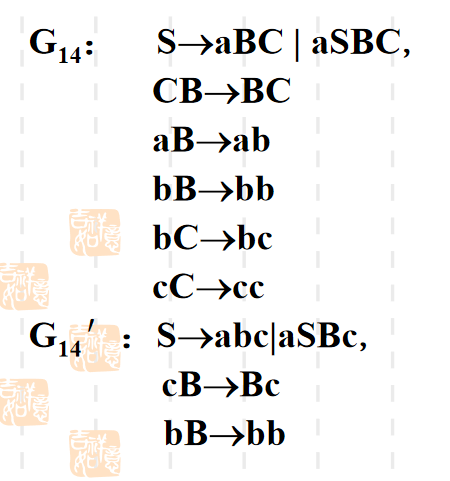
文法分类
标准
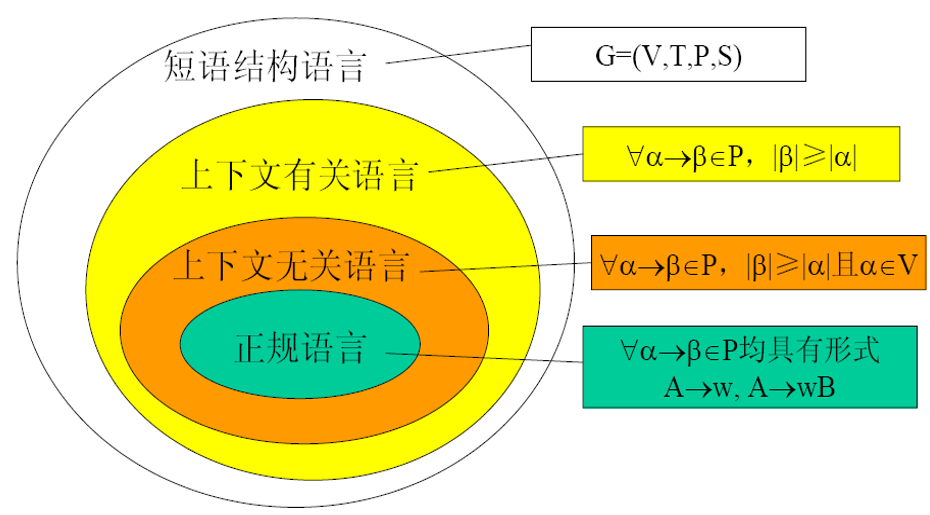

例子

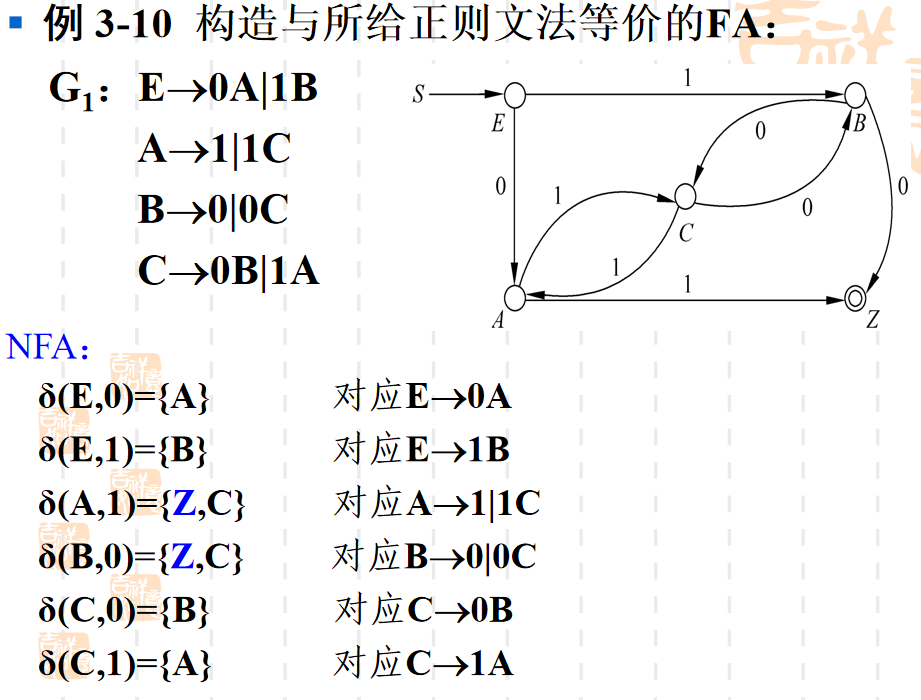
线性文法与FA的转换
右线性文法
FA -> 文法

文法 -> FA
左线性文法
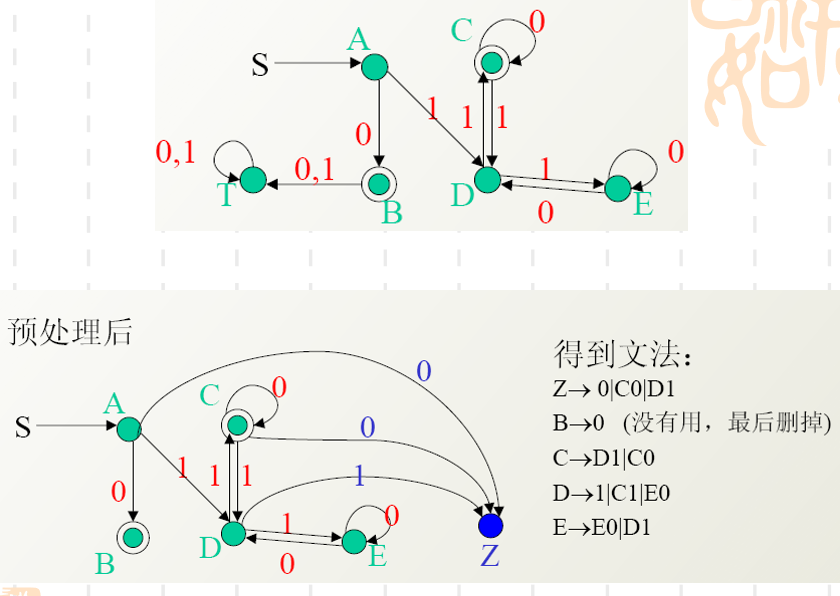
FA -> 文法
先预处理

规则:

例子
文法 -> FA
规则

例子
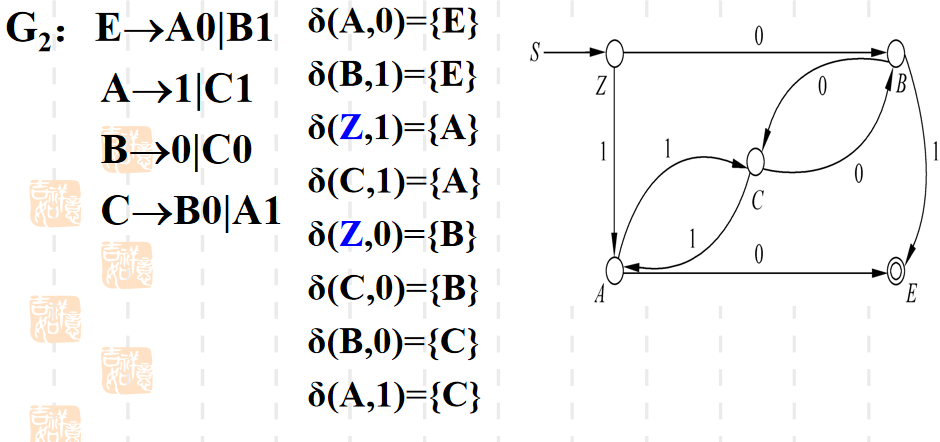
DFA、NFA、ε-NFA转换
ε-NFA -> NFA
前置知识
- = { p | 从到有一条标记为 的路}
- ε-NFA 的 状态转移函数
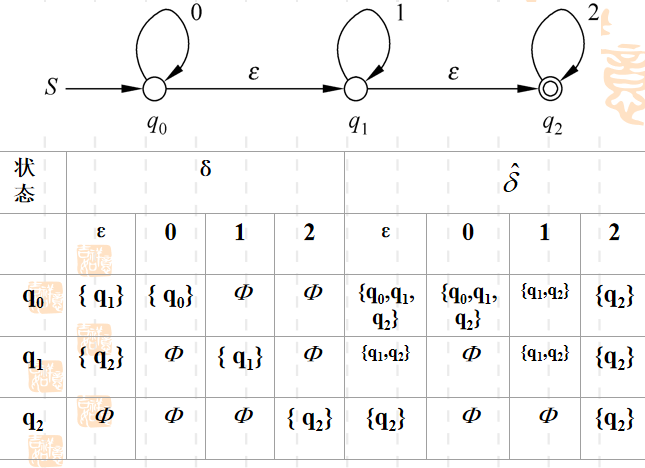
转换过程
终止状态
F 为 ε-NFA 的
F2 为转化后NFA的
转化后NFA的 转移函数
- 为 去除 ε列 的
例子
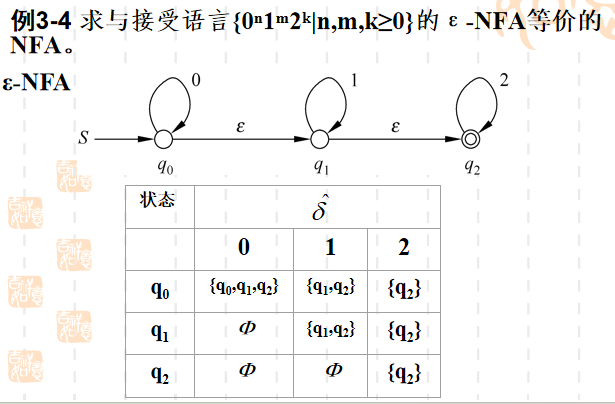

NFA -> DFA
- 带 NFA 中 终止状态 的 状态簇 为 新DFA 的终止状态
- 例子
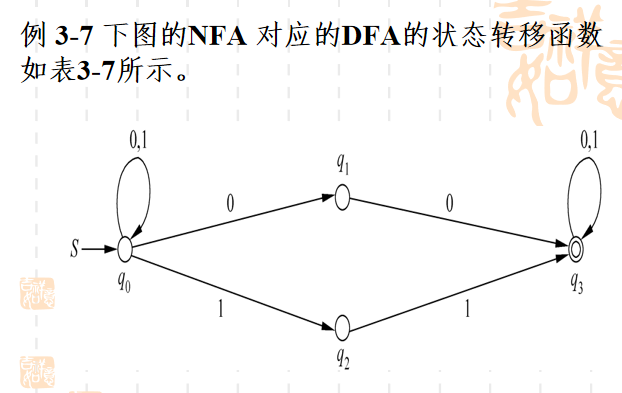
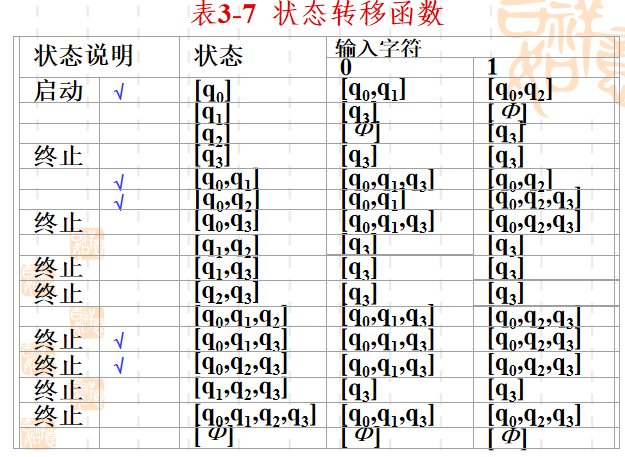
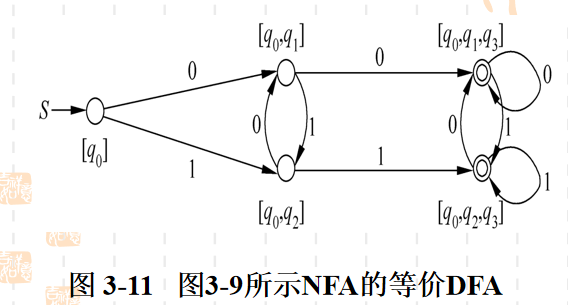
FA 与 RE 的转化
RE -> ε-NFA
n = 0
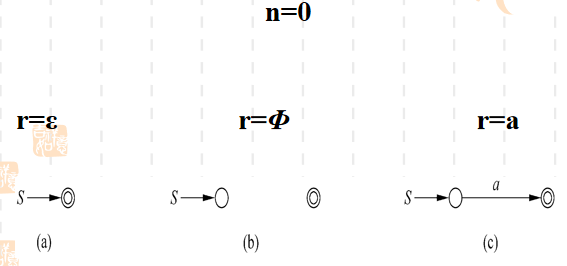
n = k+1
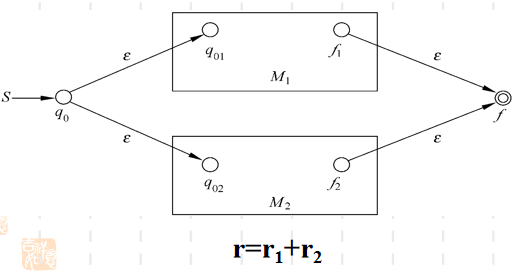
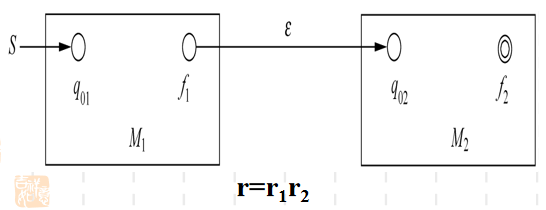
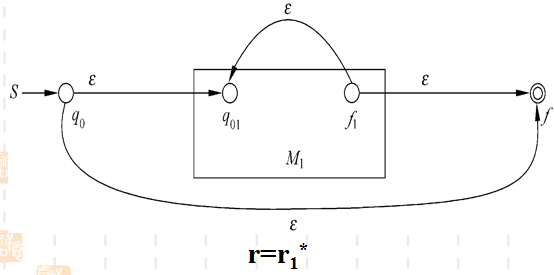
例子

DFA -> RE
例子
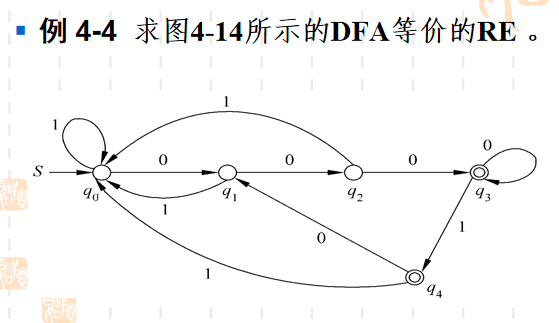
预处理:
- 用标记为X和Y的状态将M“括起来”:
在状态转移图中增加标记为X和Y的状态, 从标记为X的状态到标记为q0的状态引一条标记为ε的弧;
从标记为q(q∈F)的状态到标记为Y的状态分别引一条标记为ε的弧。 - 去掉所有的不可达状态。
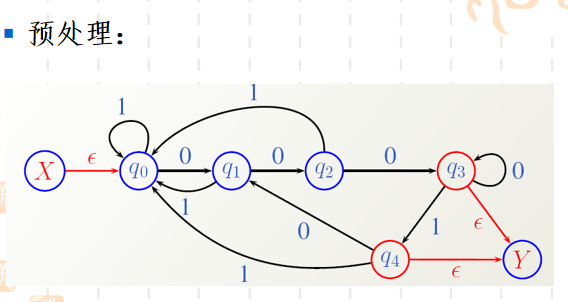
- 用标记为X和Y的状态将M“括起来”:
去掉状态q3:
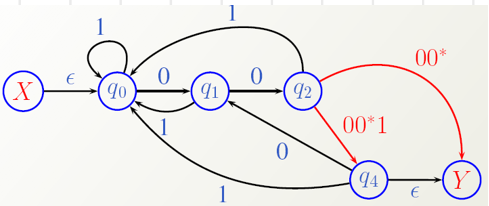
去掉状态q4
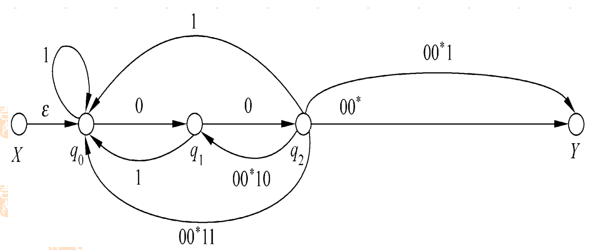
合并从标记为q2的状态到标记为Y的状态的两条并行弧。

去掉状态q0
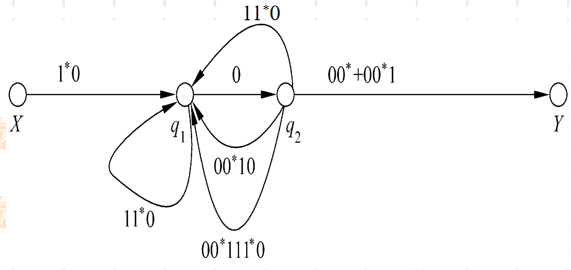
并弧
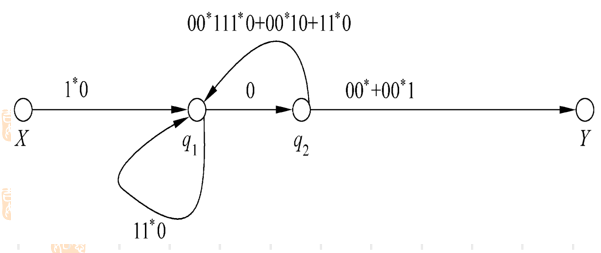
去掉状态q1
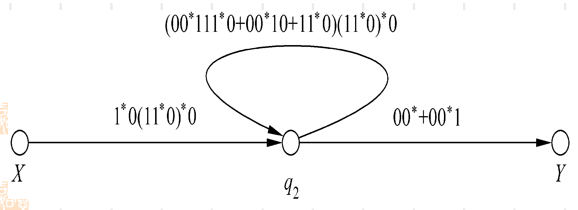
去掉状态q2
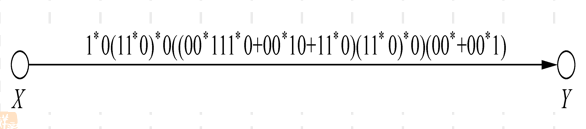
注意事项
- 不计算自身到自身的弧,如果状态q的入度为n,出度为m,则将状态q及其相关的弧去掉之后,需要添加n*m条新弧。
泵引理 与 封闭性
泵引理
定理

应用
例1

例2

例3

例4

封闭性
定义
交、并、补、连接、闭包、反转、同态、逆同态 运算都具有封闭性
补运算的封闭性
如果 是 上的RE, 那么 也是 正则的。交运算的封闭性
如果 和 是 RE, 那么 也是 正则的。同态 的定义

逆同态 的定义

例子
例1

例2

例3

Myhill-Nerode定理
定理规定以下三个命题同时成立:
- 是
- 是上的某一个具有 有穷指数 的 右不变等价关系 的 并
- 具有有穷指数
右不变等价关系
定义:设是上的等价关系,对于, 如果成立,则也成立,, 则被称为 右不变等价关系
- 关系和是 右不变等价关系
关系RM
- 设DFA M,M所确定的上的关系 定义为:
对于- 也就是说:。
- 或者说:M从开始读入x和y以后进入同一个状态。
关系RL:
- 设,L确定的Σ*上的关系 定义为:
对于
二者关系
- 如果,则 一定有
- 如果,则 不一定有
- ≤ ≤,是 的 加细
例子
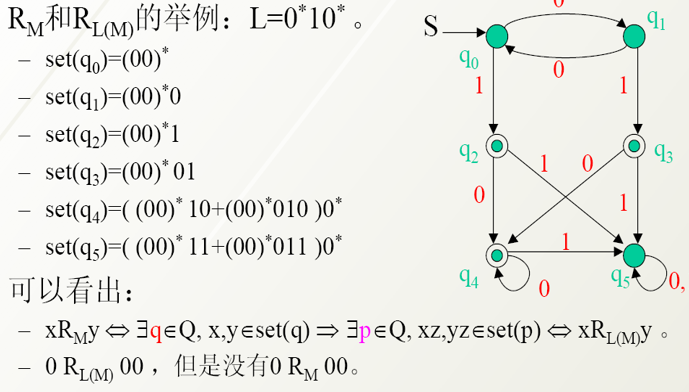
关系的指数
的指数
设是上的等价关系,则称 是 关于的指数。
的一个等价类
的关于R的一个等价类,也就是的任意一个元素
极小化
定义
最小状态DFA的含义:
没有多余状态(死状态)
- 如何消除多余状态?删除即可。
- 如何消除多余状态?删除即可。
没有两个状态是互相等价(不可区别)
- 兼容性(一致性)条件——同是终态或同是非终态
- 传播性(蔓延性)条件——对于所有输入符号,状态s和状态t必须转换到等价的状态里。
例子:
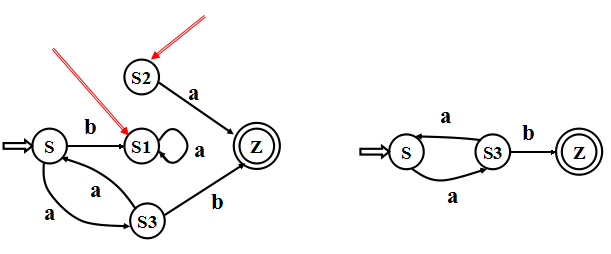
最小化下图所示的DFA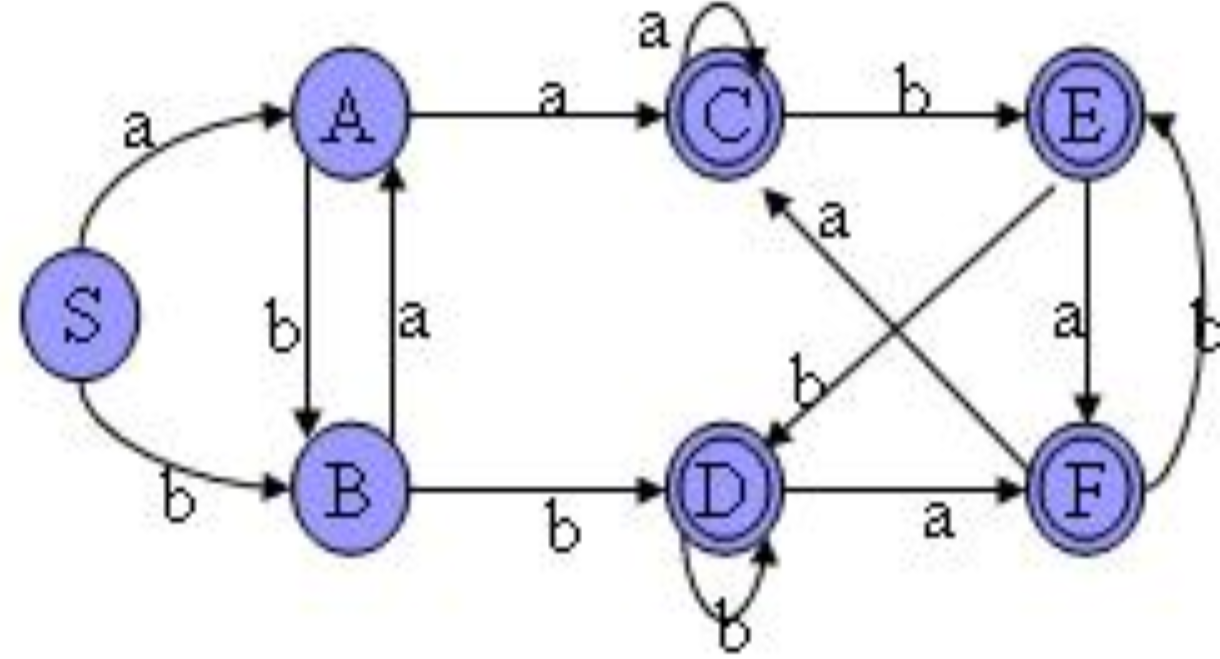
- 分成终态和非终态:
- 将M的状态分为两个子集一个由终态 k1={C,D,E,F}组成,一个由非终态 k2={S,A,B}组成。
考察{S,A,B}是否可分。
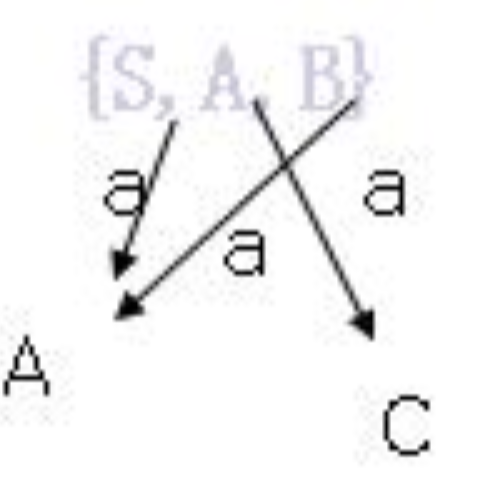
因为A经过a到达C属于k1.而S经过a到达A属于k2。B经过a到达A属于k2,所以K2继续划分为{S,B},{A}。考察{S,B}是否可再分:
B经过b到达D属于k1。S经过b到达B属于k2,所以S,B可以划分。划分为{S},{B}考察{C,D,E,F}是否可再分:
因为C,D,E,F经过 a和b 到达的状态都属于{C,D,E,F}=k1 所以相同,所以不可再分。{C,D,E,F}以{D}来代替则,因为CDEF相同,你也可以用C来代替。无所谓的最小化的DFA如图:
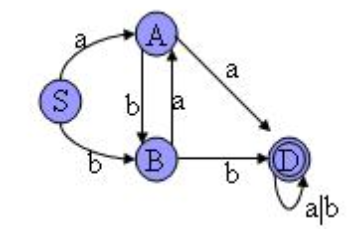
RE运算
定义
正则表达式(regular expression,RE)
- 是上的RE,它表示语言;
- 是∑上的RE,它表示语言;
- 对于,是上的RE,它表示语言;
- 如果r和s分别是∑上表示语言R和S的RE,则:
- r与s的“和” (r+s)是上的RE,(r+s)表达的语言为R∪S;
- r与s的“乘积” (rs)是上的RE,(rs)表达的语言为RS;
- r的克林闭包(r*)是上的RE,(r*)表达的语言为R*。
- 只有满足1、2、3、4的才是上的RE。
表示
- 0,表示语言{0}
- 1,表示语言{1}
- (0+1),表示语言{0,1}
- (01),表示语言{01}
- ((0+1)*),表示语言{0,1}*
运算
- 结合律:
- 分配律:
- 交换律:
- 幂等律:
- 加法运算零元素:
- 乘法运算单位元:
- 乘法运算零元素:
- $L(r*)=(L®)^* $
- 如果,则
- $L(rn)=(L®)^n $
一般地,- 幂
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Escapeey`Blog!
评论









