语法分析概述

语法分析的主要工作是根据源语言的文法，判别某个单词序列是否是源语言的一个句子

语言是满足一定组成规则的句子集合
句子是满足一定组成规则的单词序列
单词则是满足一定组成规则的字符串
这些组成规则就是文法中的产生式

两种方式

产生句子的方式：从文法的开始符号开始，逐步推导出这个单词序列，也称为自顶向下的语法分析
- 递归子程序法
- 预测分析法(LL(1))
识别句子的方式：逐步将构成程序的单词序列归约为文法的开始符号，也称为自底向上的语法分析
- 算符优先分析法
- LR(0)、SLR(1)、LR(1)、LALR(1)

无论是自顶向下还是自底向上，语法分析器都是自左到右地扫描输入单词序列，每次读入一个单词，针对输入单词序列建立一颗语法分析树
不同的分析方法对应着不同的构建树的方式

语法分析时的恢复策略

紧急方式恢复策略：丢弃输入记号，直到发现某个指定的同步记号为止。同步记号通常是定界符（分号或end标记），标志着一条新语句的开始。
短语级恢复策略：对剩余输入做局部纠正

自顶向下的语法分析面临的问题

基本思想:
- 从文法的开始符号出发，寻求所给的输入符号串的一个最左推导。
- 即从树根S开始，构造所给输入符号串的语法树
自顶向下分析实际上是一种试探性的过程，可能导致分析效率极低甚至失败
面临三种问题

二义性问题

解决方法1：改造文法，引入新的文法变量
解决办法2：根据优先级关系，保证高优先级运算符优先的原则

左递归引起的无穷推导问题

左递归: 如果存在推导 $A \Rightarrow^+ \alpha A\beta$ ，则称文法G是递归的，当 $\alpha = \epsilon$ 时称之为左递归；
间接左递归: 如果 $A \Rightarrow^+ \alpha A\beta$ 至少需要两步推导，则称文法G是间接递归的，当 $\alpha = \epsilon$ 时称之为间接左递归；
直接左递归: 如果文法G中存在形如 $A \rightarrow \alpha A\beta$ 的产生式，则称文法G是直接递归的，当 $\alpha = \epsilon$ 时称之为直接左递归。

回溯问题

文法中每个语法变量A的产生式右部称为A的候选式
如果A有多个候选式存在公共前缀，则自顶向下的语法分析程序将无法根据当前输入符号准确地选择用于推导的产生式，只能试探。
当试探不成功时就需要退回到上一步推导，看A是否还有其它的候选式，这就是回溯(backtracking)。

我们将采用提取左因子的方法来改造文法，以便减少推导过程中回溯现象的发生
当然，单纯通过提取左因子无法彻底避免回溯现象的发生。

对上下文无关文法的改造

消除二义性

改造的方法就是通过引入新的语法变量等，使文法含有更多的信息。

二义性举例：

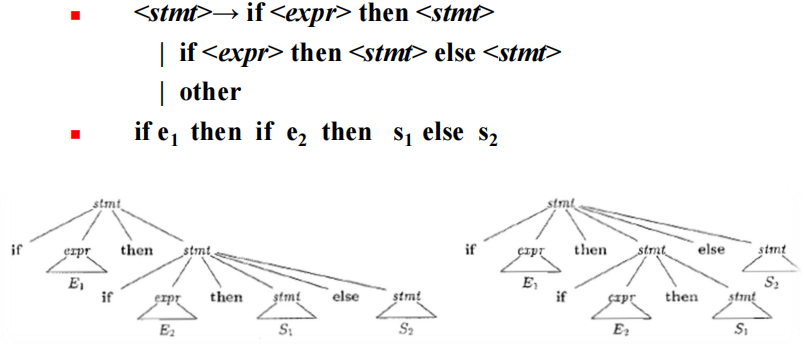
分析：
根据if语句中else与then配对情况将其分为配对的语句和不配对的语句两类。
上述if语句的文法没有对这两个不同的概念加以区分，只是简单地将它们都定义为<stmt>，从而导致该文法是二义性的
解决：

消除左递归

消除直接左递归

直接左递归的消除(转换为右递归)
引入新的变量 $A'$ ，将左递归产生式 $A\rightarrow A\alpha | \beta$ 替换为 $A\rightarrow \beta A'$ $A' \rightarrow \alpha A' | \epsilon$

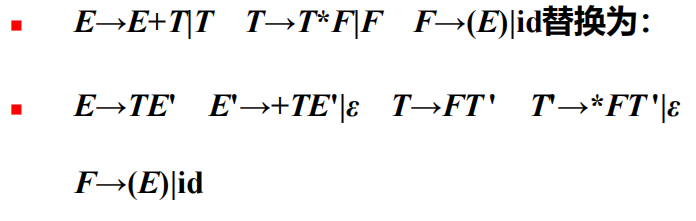
具体做法

上述方法只能消除直接左递归，无法消除间接左递归
消除间接左递归的基本思想：为语法变量编号，再采用带入法将间接左递归变为直接左递归，然后采用上述方法来消除直接左递归

消除所有左递归

提取左因子（解决回溯问题）

方法：

提取左因子并不能完全消除回溯

例子：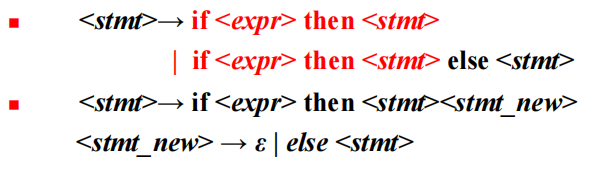

LL(1)文法

不确定的自顶向下分析
- 分析需要回溯，导致分析存在不确定性
- 代价高、效率低，实际中几乎不被采用
确定的自顶向下分析
- 不能处理所有文法，这里讨论什么样的文法可以进行确定的自顶向下分析
LL(1)文法就是可以彻底消除回溯实现确定的自顶向下分析的文法
文法要求：
- 无二义性
- 无左递归
- 任意一个语法变量A的各个候选式所能推导出的第一个终结符必须各不相同

符号串的首字符集FIRST(a)

FIRST集的定义

FIRST集的生成算法

单个符号的FIRST集的生成算法
符号串的FIRST集的生成算法

FIRST集举例

非终结符的FOLLOW集

对于\epsion的考虑，以及提出FOLLOW集的原因

FOLLOW集的定义

FOLLOW集的生成算法

FOLLOW集举例

LL(1)文法的定义

LL(1)文法举例

预测分析法

一种高效的自顶向下分析法
能够对LL(1)文法实现确定的自顶向下分析

方法综述

采用表驱动方式实现控制算法

分析表M[A,a]，即LL(1)分析表，存储执行LL(1)分析的信息，其中A是语法变量，a是输入符号。
分析栈，存放文法符号序列，#为栈底符号，初始时栈顶是开始符号
输入缓冲区，包括待分析的串和结束符
系统维持一个分析表和一个分析栈，根据当前输入缓冲区中扫描到的符号，选择当前语法变量（处于栈顶）的候选式进行推导——希望找到相应输入符号串的最左推导。

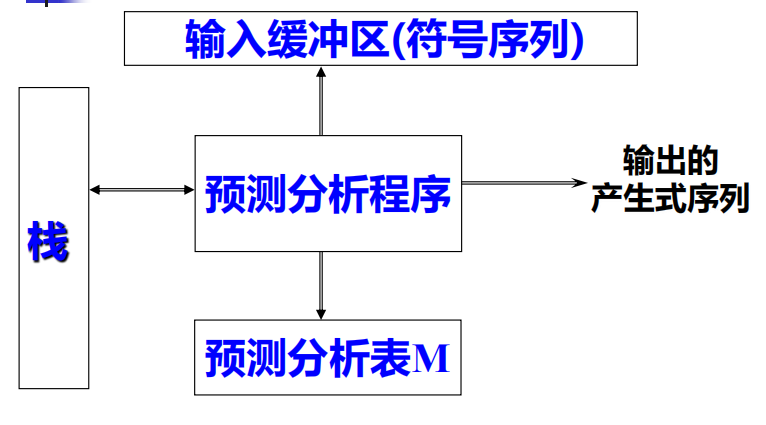
预测分析表的构造算法

预测分析法过程

实现步骤

构造文法
改造文法：消除二义性、消除左递归、提取左因子
求每个候选式的FIRST集和变量的FOLLOW集
检查是不是LL(1)文法
若不是 LL(1),说明文法的复杂性超过自顶向下方法的分析能力，需要附加新的“信息”
构造预测分析表
实现预测分析器

预测分析控制过程

在系统启动时，输入指针指向输入串的第一个字符，分析栈中存放着栈底符号#和文法的开始符号
根据栈顶符号A和读入的符号a，查看分析表M,以决定相应的动作。
- 如果 A=a=#，分析成功并停机
- 如果 A=a≠#，弹出栈顶符号A，并将输入指针指向下一个符号
- 如果A是语法变量，程序访问分析表M的**M[A,a]**表项，该表项或者是一个A产生式，或者是出错信息。
- 如果M[A,a]={A→UVW}，则用WVU(栈顶)替换原栈顶符号A，输出该产生式

算法实现

算法4.5 预测分析程序的总控程序
输入：输入串w和文法G=(V, T, P, S)的分析表M;
输出：如果w属于L(G)，则输出w的最左推导，否则报错;
步骤：
将栈底符号#和文法开始符号S压入栈中;
repeat
    X:=当前栈顶符号; a:=当前输入符号;
    if X∈T∪{#} then
        if X=a then
            if X≠# then
                将X弹出栈;
                前移输入指针; 
        else //当前栈顶终结符和当前输入符号不一致
            error
    else //也就是X属于一个语法变量
        if M[X, a] = Y1Y2…Yk then 
            将X弹出栈;
            依次将 Yk，…，Y2，Y1 压入栈;
            输出产生式 X → Y1Y2…Yk;
        else 
            error
until X=#

预测分析法举例

文法、FIRST集和FOLLOW集
实现的预测分析表
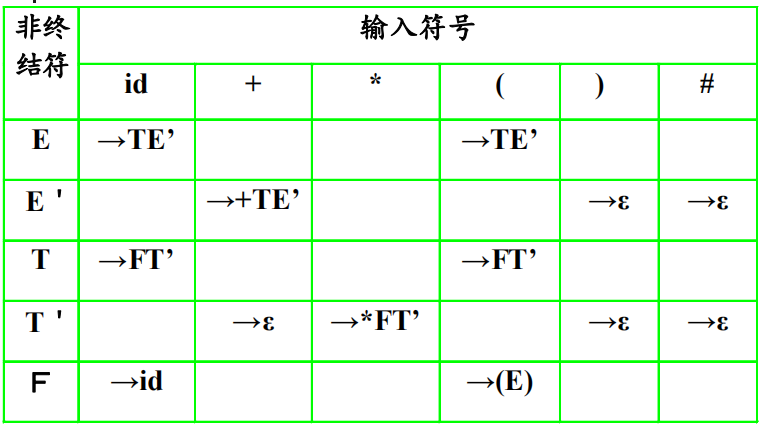
对输入串 id+id*id 进行分析的过程

输出的产生式序列形成了最左推导对应的分析树

预测分析中错误的处理

错误类型

- 栈顶终结符号和下一个输入符号不匹配
- 栈顶是语法变量A，a是下一个输入符号，M[A, a]是空白表项

紧急方式错误恢复策略

发现错误时跳过一些输入符号，直到下一个语法成分包含的第一个符号为止 （同步记号）

同步记号的一般选择策略：对语法变量A，如果M[A,a]无定义，并且a属于FOLLOW(A)，则增加M[A,a]为 “同步点”(synch)。当程序到达这个同步点时，放弃对A的识别，而转入分析A后面的符号。

错误的处理步骤：

对预测分析表添加同步点
预测分析执行过程中加入以下判断
- 如果表项M[A, a]为空，则跳过输入符号a；
- 如果表项M[A, a]是synch，则弹出栈顶的语法变量并试图恢复分析；
- 如果栈顶的记号与输入符号不匹配，则从栈顶弹出该记号。

错误的处理举例

对预测分析表添加同步点

处理过程

递归下降分析法

所谓递归下降分析法，是指根据各个候选式的结构，为文法的每个语法变量编写一个处理程序，用来识别该语法变量所代表的语法成分