为什么使用四元数

  • 欧拉角的缺点
    • 同一旋转的表示不唯一
    • 万向节死锁(Gimbal Lock)

      • 当某个特定轴到达某个特殊值时，绕一个轴旋转可能会覆盖住另一个轴的旋转，从而失去一维自由度

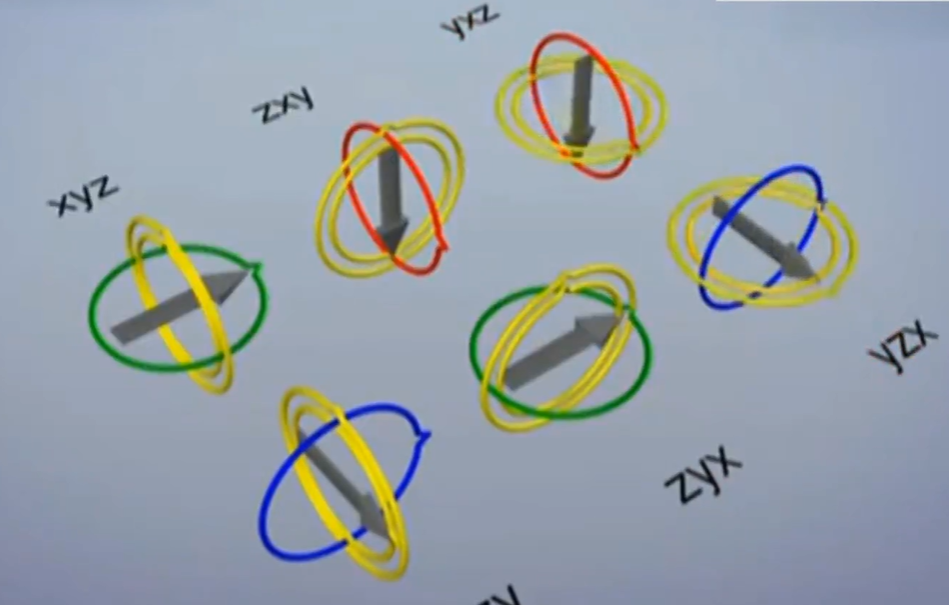
      • 最外层和最内层的旋转轴重合

      • 例如 Unity中X轴达到90度时就会发生

  • 四元数不存在万向节死锁的问题

四元数是什么

定义

  • 形如ai+bj+ck+dai+bj+ck+d的数字，a,b,c,da,b,c,d是实数
    • 可以看作一个四元数包含了一个标量和一个3D向量
    • [w,v][w,v],ww为标量，vv为3D向量
    • [w,(x,y,z)][w,(x,y,z)]
  • 对于给定的任意一个四元数：表示3D空间的一个旋转量

轴-角对

  • 在3D空间中，任意旋转都可以表示绕着某个轴旋转一个旋转角得到(该轴是任意一个轴，不一定是x,y,zx,y,z轴)

四元数旋转

  • 对于给定旋转，假设绕着nn轴，旋转β\beta度，nn轴为(x,y,z)(x,y,z)，那么可以构成四元数为
    • 四元数q=[cos(β/2),sin(β/2)n]q = [cos(\beta/2),sin(\beta/2)n]
    • 四元数q=[cos(β/2),sin(β/2)x,sin(β/2)y,sin(β/2)z]q = [cos(\beta/2),sin(\beta/2)x,sin(\beta/2)y,sin(\beta/2)z]
      这里一定为β/2\beta/2
  • 四元数q表示绕着轴nn，旋转β\beta度的旋转量

Unity中的四元数

QuaternionQuaternion是Unity中表示四元数的结构体

初始化

轴角对公式初始化

  • 方法一 (为计算原理，不用)
    四元数q=[cos(β/2),sin(β/2)x,sin(β/2)y,sin(β/2)z]q = [cos(\beta/2),sin(\beta/2)x,sin(\beta/2)y,sin(\beta/2)z]
1
2
//假设绕(1,0,0)旋转60度
Quaternino q = new Quaternino(Mathf.Sin(30 * Mathf.Deg2Rad), 0, 0, Mathf.Cos(30 * Mathf.Deg2Rad));
  • 方法二 (封装的方法)
1
2
//假设绕(1,0,0)旋转60度
Quaternino q = Quaternino.AngleAxis(60, Vector3.right);

四元数和欧拉角转换

  • 欧拉角转四元数 (静态方法)
1
Quaternino q = Quaternino.Euler(60, 0, 0);
  • 四元数转欧拉角 (成员属性)
1
print(q.eulerAngles)

四元数弥补欧拉角缺点

四元数相乘代表旋转四元数

  • 解决同一旋转的表示不唯一
    四元数旋转角度始终在(−180o∼180o)(-180^o\sim180^o)之间

  • 解决万向节死锁(Gimbal Lock)
    在万向节死锁时仍然可以通过四元数乘法来使物体绕自己指定的轴旋转

  • tips:以下代码在界面上rotation = (90,0,0)的前提下演示，此时万向节已经死锁

1
2
3
4
5
// 提示：这里的Vector3.up代表的是本地坐标系的y轴,不是世界坐标系的
void Update()
{
    this.transform.rotation *= Quatenion.AngleAxis(1, Vector3.up);
}

对比欧拉角，这个会出现万向节死锁

1
2
3
4
5
6
7
Vector3 e;
void Update()
{
    e = this.transform.rotation.eulerAngles;
    e += Vector3.up;
    this.transform.rotation = Quatenion.Euler(e);
}

四元数的常用方法

单位四元数 用于初始化对象

Quatenion.identity

  • 当角度为0或者360度时
  • 单位四元数表示没有旋转量
  • 对于任何给定轴都有单位四元数
  • [1,(0,0,0)][1,(0,0,0)]和[−1,(0,0,0)][-1,(0,0,0)]都是单位四元数表示没有旋转量
1
2
3
print(Quatenion.identity);
//实例化时使用
Instantiate(testObj, Vector3.zero, Quaternion.identity);

四元数插值运算

Quaternion.Slerp()

result=start+(end−start)∗tresult = start + (end-start) * t

1
Quaternion.Slerp(start, end, t);
  • 四元数同样提供如同Vector3的插值运算LerpLerp和SlerpSlerp
  • 二者区别不大,SlerpSlerp效果好一些，建议使用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void Update()
{
    //1. 无限接近 先快后慢
    A.transform.rotation = Quaternion.Slerp(A.transform.rotation, target.rotation, Time.deltaTime);

    //2. 匀速变化 time>=1到达目标
    //这种匀速移动 当time>=1时 当目标位置改变后 他会直接瞬间变到目标的角度 所以加入以下判断
    if(nowTarget != target.rotation)
    {
        nowTarget = target.rotation;
        time = 0;
        start = B.rotation;
    }
    time += Time.deltaTime;
    B.trainsform.rotation = Quaternion.Slerp(start, nowTarget, time);
}

向量指向转四元数

Quaternino.LookRotation(面朝向量)

  • LookRotationLookRotation方法将传入的面朝向量转换为对应的四元数角度信息

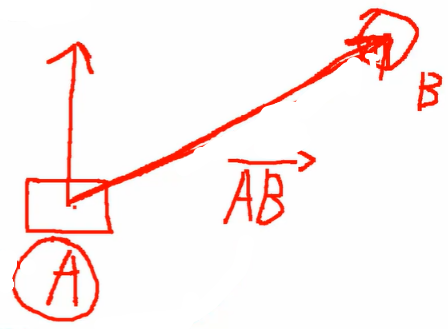
  • 举例：当AA面朝向想改变时，只需要把AA和BB之间的向量AB→\overrightarrow{AB}传入该函数，便可以得到目标四元数角度信息，之后将AA四元数角度信息改为得到的信息即可转向

1
2
Quaternion q = Quaternion.LookRotation(B.position - A.position);
A.rotation = q;

四元数计算

四元数相乘

  • 两个四元数相乘得到一个新的四元数，代表两个旋转量的叠加
  • 相当于旋转
  • 注意：旋转相对的坐标系 是物体自身坐标系
1
2
Quaternion q = Quaternion.AngleAxis(20, Vector3.up);
this.transform.rotation *= q;

四元数乘向量

  • 四元数乘向量返回一个新向量
  • 可以将指定向量旋转对应四元数的旋转量，相当于旋转向量
  • 注意：一定是四元数乘向量 先后顺序不能改变
1
2
Vector3 v = Vector3.forward;
v = Quaternion.AngleAxis(45, Vector3.up) * v;
  • 实例：比如做弹幕类游戏，现有一个弹幕的方向，则可通过乘四元数旋转得到一圈弹幕的方向